Матрицы Матрица - прямоугольная (в частном случае квадратная) таблица с числами. Матрица m × n - это таблица из m строк и n столбцов. Если m = n, матрицу называют квадратной матрицей порядка n. Пример матрицы 4×3 : a1,1   a1,2   a1,3   a2,1   a2,2   a2,3   a3,1   a3,2   a3,3   a4,1   a4,2   a4,3   Определитель матрицы Определитель матрицы A (обозначается как det A) это число, которое ставится в соответствие матрице A по определенному правилу. Определитель существует (определен) только для квадратной матрицы. Определителем квадратной матрицы A порядка n называется число: det(A)= = 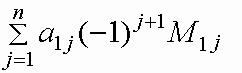где M1,j - определитель квадратной матрицы порядка n -1, полученной из матрицы A вычеркиванием первой строки и j -го столбца, называемый минором элемента a1,j. Выражение det A = 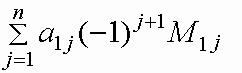называется формулой вычисления определителя разложением по первой строке. Число (-1) j+1 M1,j называется алгебраическим дополнением элемента a1,j. Если вас пугает это формула, то она значит следующее: Определитель вычисляется как сумма n слагаемых, где n - порядок матрицы. Знак, с которым каждое слагаемое входит в сумму, определяется как (-1)1+k. Каждое слагаемое представляет собой произведение двух чисел: элемента первой строки матрицы на минор - определитель матрицы, получаемой из исходной путем вычеркивания 1 строки и j столбца. Обратите внимание, что порядок минора на 1 меньше, чем у исходной матрицы!!! Умножение матриц Произведением матриц A размером m × n и матрицы B размера n × k называется матрица размера m × k, элементы которой определяются формулой ci,j = n a i,q · b q,j ∑ q=1 i=1, ... , m j=1, ..., k Произведение матриц записывается как C=A·B. Произведение матриц определено, если число столбцов матрицы A равняется числу строк матрицы B!!!! Для более легкого запоминания формулы умножения матриц существует простое правило: строка на столбец. Берем элементы из строки матрицы А и они умножаются на соответствующие элементы столбца матрицы B. Потом все произведения складываются и мы получаем значение элемента матрицы C. Координаты элемента в результирующей матрице определяется как номер строки матрицы A и номер столбца матрицы B. Транспонирование матриц Транспонирование матрицы - это такая операция над матрицей, когда первая строка становится первым столбцом, вторая строка становится вторым столбцом и так далее... В результате получается транспонированная матрица, обозначаемая как AT. Обратная матрица Матрица A-1 - называется обратной к матрице A, если выполняется условие A ·A-1 = A-1·A=E. Для квадратной матрицы A обратная матрица существует тогда, когда det A ≠ 0. Обратную матрицу находим следующим образом:   где Ai,j - алгебраические дополнения элементов матрицы A.