Метод разложения матрицы по первой строке
Определитель матрицы nxn задаётся формулой:
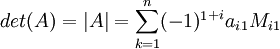
где M1k - определитель матрицы, получаемой из исходной путем вычеркивания 1 строки и k столбца.
Если вас пугает это формула, то она значит следующее:
1. Определитель вычисляется как сумма n слагаемых, где n - порядок матрицы.
2. Знак, с которым каждое слагаемое входит в сумму, определяется как (-1)1+k.
3. Каждое слагаемое представляет собой произведение двух чисел: элемента первой строки матрицы на минор - определитель матрицы, получаемой из исходной путем вычеркивания 1 строки и k столбца.
Обратите внимание, что порядок минора на 1 меньше, чем у исходной матрицы!!!
Хватит болтать, погнали матрицы считать
|